Following the Bouncing Sphere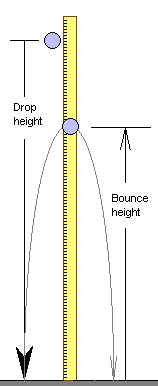

Experimental Procedure

1. Write down the type of sphere: ____________________________
2. Hold the sphere center 20 centimeters above the table in front of a vertical meter stick.
3. Drop the sphere, measuring the height of the first bounce only.
4. Record the drop height and first bounce height in centimeters in the table below.
5. Repeat the procedure for 40 cm, 60 cm, 80, and 100 cm.

6. Table

   Drop Height/cm	Bounce Height/cm
   0	0
   20	____________
   40	____________
   60	____________
   80	____________
   100	____________

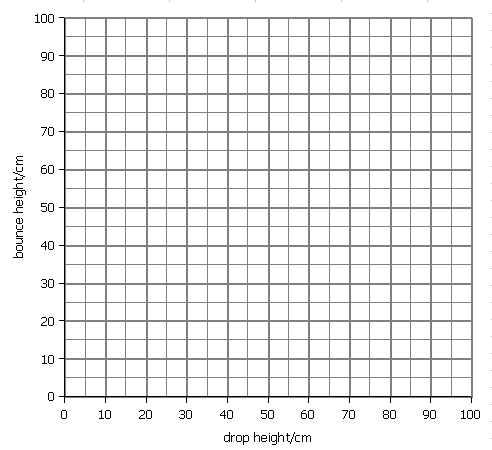
7. Graphing the Data

   Graph the drop height in cm on the x-axis and the bounce height in cm on the y-axis.
   

8. Calculations

   Fit a best line to the points starting at the origin (0,0).
9. Determine the slope.
   1. Pick an intersection the line passes through close to the upper right corner of the graph.
   2. Determine the coordinates of the upper right point
      

      (_____, ______)
         x      y

   3. Use the formula for determining the slope from the point:
      
      slope m = y/x =
10. slope m = __________________
11. Write the type of sphere and the slope on the board.
12. ________ Use the slope to calculate how high the sphere would bounce if dropped from 200 centimeters. Use the slope you calculated above.
13. ________ Does a bouncier sphere such as a superball have a larger or smaller slope than a less bouncy sphere?
14. ________ What would be the slope for an object that does not bounce, such as a book?
15. ________ Could a sphere have a slope of two?
16. ________ What is the largest possible slope?

Copyright ©2000 College of Micronesia-FSM. • Laboratory revised: 07 March 2000, 24 March 2003.